Game theory and disarmament have a long and rich history together. Though the logic of game theory has been used for millennia, it was not formalized until the violence of World War II, and the nascent field was popularized extensively during the Cold War (Ross 1997). Indeed, it was pursued mainly for military purposes, especially to model the nuclear arms race between the Soviet Union and the United States (Kuhn 1997). These models were studied “exhaustively” during the Cold War, and they led to a rich body of literature and theory that has become integral to economics, philosophy, mathematics, international relations, business, and evolutionary biology (Ross 1997). However, despite its deep history with disarmament and increased popularity, game theory seems to have declined in literature on disarmament (O’Neill 1990: 20). The current landscape in international politics is much harder to model in game theoretical terms, but game theory can still prove valuable for developing approaches to encourage disarmament.

In this paper, I aim to use game theory in discussing disarmament by exploring a model of disarmament that looks beyond the payoff table and incorporates experimental economics, and I will present a plan to turn this game theoretical concept into a practical solution. To include those who may be unfamiliar with the field, I will begin with an introduction to game theory and how it has been applied to disarmament. Next, I will explore the most promising model, the Stag Hunt, and I will incorporate experimental economics to compliment the insights of game theory. This will allow me to introduce an incentive scheme to facilitate disarmament, something I call “disarmament bonds.” Finally, I will conclude with an afterword on the importance of disarmament for eliminating the scourge of war from the planet and providing prosperity for all.

Background

“[G]ame theory is the science of strategy” (“Game theory”). It is the mathematical modeling of situations (games) where two or more parties (players) make decisions that impact one another (Myerson 1997). As Myerson explains, “Game theorists try to understand conflict and cooperation by studying quantitative models and hypothetical examples” (1997: 2). Models can identify key reasons why agents might make certain decisions or adopt certain strategies. However, models of reality are just that—models. They may ignore key features of reality and oversimplify situations, and thus caution must be exercised in using game theory to make policy decisions (Dixit, Skeath, & Reiley 2015: 37).

To examine old approaches to disarmament and game theory, it is first necessary to understand several basic games. The most famous among these is the Prisoner’s Dilemma, first studied by RAND because of implications for the nuclear arms race (Kuhn 1997). In its formal game-theoretical definition, a Prisoner’s Dilemma is a symmetric, two-player, simultaneous game where players face the choice to cooperate or defect. The “temptation” payoff to unilaterally defect must be the highest, followed by the “reward” payoff for mutual cooperation, then by the “punishment” payoff for mutual defection, and finally by the “sucker’s” payoff for unreciprocated cooperation. Thus a Prisoner’s Dilemma will generally have payoffs structured as follows, where T > R > P > S (Kuhn 1997):

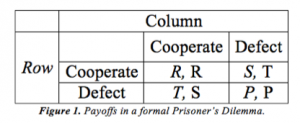
Another important game is the Stag Hunt (sometimes called an assurance, coordination, or reciprocity game). The story comes from enlightenment philosopher Jean Jacques Rousseau’s idea of the social contract (Jervis 1978: 167). In his story, there are two hunters. If they both work together, they can hunt a stag, which yields plenty of meat (Jervis 1978: 167). The stag cannot be hunted successfully alone. However, individuals can hunt hare successfully (Jervis 1978: 167). Hare yield less meat, and there are a limited number of them (Jervis 1978: 167). If both hunt hare, they split the available game, but if one hunts hare while the other pursues the stag, then he/she will have no competition and can successfully hunt all the rabbits (Jervis 1978: 167):The payoffs in the Prisoner’s Dilemma cause both players to defect, which means (defect, defect) is the game’s equilibrium (Dixit, Skeath, & Reiley 2015: 100).  The important takeaway from the Prisoner’s Dilemma is that players’ pursuit of self-interest leaves everyone worse off (Axelrod 1984: 9).

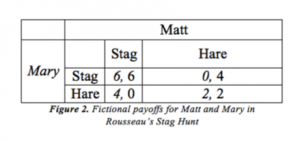
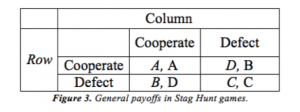
This game has two equilibria: one is when both hunt the stag, and the other is when both hunt hare (Dixit, Skeath, & Reiley 2015: 113). Both players want to assure they can reciprocate the move of the other. The formal definition of a Stag Hunt is modeled by the following payoff table where A > B ≥ C > D (Engelmann 1994: 323-324):

Finally, it is also important for disarmament to examine a rarer game: Deadlock (sometimes called Prisoner’s Delight). In Deadlock, both players’ pursuit of self-interest actually leads to the most mutually beneficial outcome. The payoff matrix looks something like the following, where numbers represent utility:

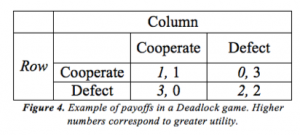
Here, like in the Prisoner’s Dilemma, the equilibrium is when both players defect (Hansel, Mutschler, & Dickow 2018: 47). Unlike in the Prisoner’s Dilemma, this is actually the most mutually beneficial outcome for the players. (This is not, however, the most beneficial outcome for society.)

Old Disarmament Models

With these games having been understood, we can now examine how they have been applied to disarmament. First, consider the Prisoner’s Dilemma. An arms race can be modeled by a Prisoner’s Dilemma when two states share these values: (1) they both prefer to be the state with more weapons, (2) they are terrified of being the state with fewer weapons, and (3) they would prefer both being less armed than both being more armed (because of the cost of weapons and the destructive capabilities should war break out) (Mutschler 2013: 42). When states share these values, their pursuit of being the state with more weapons will cause the less desirable outcome of both parties increasing their arms.

A Stag Hunt is the appropriate model when both countries realize that mutually disarming is more desirable than unilaterally arming (Engelmann 1994: 323). When disarmament can be modeled by a Stag Hunt, both states understand that they can feel secure if both countries don’t increase their arms; they view unilateral armament as bringing little increase in security and being costly. However, they still would rather be the state to unilaterally arm than to be the state “tricked” into disarming. This often drives both states to arm, which is viewed as less desirable than mutual cooperation.

Finally, Deadlock is an appropriate model when both states value mutually arming (Mutschler 2013: 42-43). It is generally believed that states acquire these values when they want to retain their status as a strong military power, especially if they are nuclear states (Picardo 2018).

 Previous Approaches to the Games

The Prisoner’s Dilemma is most often bypassed by using enforcement authorities (Dixit, Skeath, & Reiley 2015: 390), which changes the actual payoffs so as to change the game itself. Repeated play with the same opponent (iteration) is also propitious for achieving cooperation (Axelrod 1984). When play is repeated, agents have to account for future iterations (Axelrod 1984: 11). If a player defects, she is making cooperation much more difficult in the future. If the future is valued highly enough, then players will seek cooperation (Axelrod 1984: 126). If this is reciprocated, then cooperation will continue; if not, then players should defect in response (Axelrod 1984: 22). This strategy of reciprocating the move of your opponent is called Tit-for-Tat, and it is a valuable tool for escaping Prisoner’s Dilemmas (Axelrod 1984: 31).

For the Stag Hunt, communication and credibility are the most important factors in finding a solution. If players have met before or players know each other’s background, then trust can sometimes be established. Communication is an important tactic for coordination, but communication becomes less useful as players’ interests are less aligned (Dixit, Skeath, & Reiley 2015: 284). In many real-world scenarios, verification and monitoring can supplement communication to ensure cooperation (Mutschler 2013: 44).

Deadlock is the most difficult game to address, as both players are content with the outcome of the game. The only way to change a Deadlock situation is to change the values of the players themselves (Hansel, Mutschler, & Dickow 2018: 48). Though this is a difficult task, it is not impossible, and epistemic communities can play an influential role in molding the values (Mutschler 2013: 60).

These are the game theoretical solutions to moving towards cooperation, but they have not been as successful as might be hoped in bringing about multilateral cooperation in disarmament. Though the models can fit the true attitudes states have towards disarmament, the theoretical solutions have not been enough to further disarmament in reality.

Outside the Box

The UN Conference on Disarmament is the UN’s multilateral disarmament forum based in Geneva (UNOG). It has been in existence since 1979 and has seen successes (UNOG), but it has been thoroughly deadlocked for the past 20 years (Swissinfo 2018). Disarmament scholars make thorough and exciting cases on the benefits of disarmament, and many use the work of Axelrod to show that cooperation is possible without an enforcement mechanism (1984). Others focus on shifting Deadlock games to Prisoner’s Dilemmas to allow Axelrod’s insight on iteration to solve the problem (Hansel, Mutschler, & Dickow 2018: 47-48). These solutions have been tried: countries have interacted with each other repeatedly, they have engaged in extensive communication, and epistemic communities have been contributing vociferously to try to change values. But game theory’s lessons on cooperation have not been realized to date. Disarmament negotiations are in desperate need of new, creative approaches (Borrie & Randin 2006: 3). It is time to reevaluate the old game-theoretical approaches, modify them, and think outside the payoff tables to see how we can galvanize multilateral disarmament in reality.

Modifying the Approach and Looking Beyond the Payoff Tables

The classic disarmament models all view disarmament as two-player games. Multilateral interactions, however, involve far more players, and they are thus a class of games called collective-action games. The model for these games are derived from mathematical equations, but the key takeaways actually don’t require looking at the formulas. The collective-action model that is most auspicious for cooperation is a multiplayer model of the Stag Hunt. In collective-action Stag Hunts, the equilibrium depends on how many players are involved and the moves they make (Dixit, Skeath, & Reiley 2015: 430). The more players cooperate, the bigger the incentive for others to follow suit. (Dixit, Skeath, & Reiley 2015: 430). Furthermore, as the number of people in the group decreases, individuals are more likely to choose cooperation (Dixit, Skeath, & Reiley 2015: 430). This has been shown both mathematically and experimentally, and repeated local interactions are far more likely to engender cooperation (Keser, Ehrhart, & Berninghaus 1998: 269).

Game theory tells us that there are two equilibria in the Stag Hunt. In particular, these are Nash Equilibria, meaning that no player would retroactively choose to unilaterally change their move once in equilibrium. Take another look at the Stag Hunt in the table below:

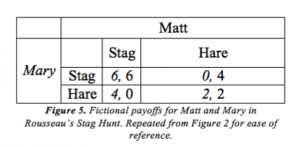
The two Nash Equilibria are (stag, stag) and (hare, hare). In (stag, stag), neither Matt nor Mary would change their move, as both would decrease their payoff from 6 to 4. Similarly, in (hare, hare), changing moves would decrease the payoff from 2 to 0, so this is also a Nash Equilibrium. Game theory, payoff tables, and equilibria are supposed to shed light on what players should do given certain scenarios, and they are supposed to give insight as to what might happen. Having two Nash Equilibria, however, is not very helpful in this regard; indeed, there is still some doubt as to the true value of Nash Equilibria (Cassidy 2015). To understand how players approach the Stag Hunt, we need to explore two alternative types of equilibria and use experiments to determine when and why they are chosen.

In the Stag Hunt, the (stag, stag) equilibrium is the payoff dominant equilibrium, meaning it produces the best overall payoffs for both players (Polena 2014: 8). The risk dominant equilibrium is (hare, hare), as it is the outcome that occurs when players make moves to minimize risk (Polena 2014: 8). This is an important distinction, as it not only describes the equilibrium established, but also why that strategy was pursued.

As might be expected, the literature yields conflicting accounts as to which strategy is pursued more (Polena 2014: 21). Many economists have run experiments to determine which equilibrium players will pursue, and while they have not conclusively shown that one is more common than the other, they have shown how players can be influenced to move towards one equilibrium or another (Polena 2014: 22). Unlocking cooperation in the Stag Hunt requires looking at the relative values of the payoffs. Manipulating these relative payoffs can encourage players to pursue payoff dominance or risk dominance (Siang 2010: 2).

If Mary chooses to hunt the stag and Matt chooses to hunt hare, then Mary gets nothing while Matt gets a payoff of 4. Mary cooperated, but Matt did not. If Mary had refused to cooperate, she would have instead gotten a payoff of 2. The difference between Mary’s payoffs in these two scenarios is called the cooperation cost (Siang 2010: 1). It is the amount one stands to lose by unilaterally cooperating in the Stag Hunt, and it plays a significant role in influencing the strategies of players in the Stag Hunt (Siang 2010: 1). The smaller the cooperation cost, the more likely cooperation is to happen (Siang 2010: 6). Otherwise, a large cooperation cost drives players to pursue their risk-minimizing strategy (Siang 2010: 6). Furthermore, players do not respond to increases in payoffs in the payoff-dominant equilibrium alone (Dubois, Willinger, & Van Nguyen 2011: 375). Even if hunting the stag will bring massive payoffs to both players, the driving factor will still be the amount of risk present.

By looking beyond the payoff tables, we can gather valuable information from experimental economics as to what conditions make cooperation more likely. Multiplayer Stag Hunts offer two equilibria: one maximizes benefits, the other minimizes risk. Small, localized groups where players repeatedly interact allow for the cooperative equilibrium to be realized, and decreasing the risk taken by cooperating also incentivizes players to work together to maximize benefits. Increases in payoffs for mutual cooperation alone are not effective for inducing cooperation.

Incentivizing a Solution

Based on these revelations, the focus among disarmament advocates should be geared towards states with two characteristics. First off, these states must have several relative values. They must value mutual disarmament more than unilateral armament; this comes from recognizing that arming oneself has a hefty financial and economic opportunity cost and that mutual disarmament can bring security to the state. The countries also need to value mutual disarmament above mutual armament. (This is generally understood, as arms are costly and relative security isn’t increased when both states choose to arm.) Second, these states should be a part of a small group of other countries with the same values that interact with each other repeatedly.

The perspective of states with these characteristics on disarmament can be modeled successfully as a collective-action Stag Hunt. As discussed earlier, in order to encourage cooperation in this scenario, risk must be decreased. To do this, I propose an agreement utilizing what I call “disarmament bonds.” The basic architecture would involve multiple states first paying a sum of money up front and agreeing to disarm. If a state disarms, it receives its money back plus interest. If it fails to uphold the agreement, then it loses its investment.

The initial payment would be akin to purchasing a bond: the states could choose maturity dates, levels of disarmament, and number of interest payments, which would then be used to calculate the yield rate. States would be allowed to pay for military salaries, any civilian services that fall under the defense budget (like natural disaster relief or education programs), and administrative costs. Over the course of the maturity period, states would have to meet strict benchmarks for disarmament (agreed to ahead of time), and an independent party would be established to verify and inspect disarmament progress and military spending. Interest would accrue as disarmament benchmarks are met, and as long as a state upholds the agreement until the end of the maturity period, the principal amount would be returned in full. Failure to disarm would trigger a default on the bond, and that state would lose its principal sum and all future interest payments.

Consider the payoff tables below to see how this scheme would decrease risk in the Stag Hunt model of disarmament. Though this is presented in the table as a two-player game for ease of reference, the concept and mathematics still hold in the collective-action model (Dixit, Skeath, & Reiley 2015: 424):

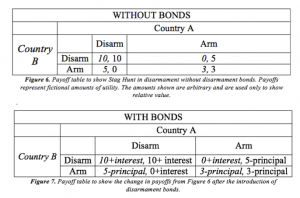
Even without being able to quantify payoffs to each state, we can see that the structure of disarmament bonds brings down cooperation costs. The contract of earning interest for disarming and losing principal for arming decreases the cooperation cost, which in turn increases the chances of cooperation.

This plan has another benefit, as pointed out during a private conversation: it can help cooperation withstand the test of leadership changes (Private meeting, 2018). If a country purchases a five-year disarmament bond, the bond has already been purchased by the state, and thus new political leaders can reverse disarmament policy only at the cost of losing the principal and future interest payments. This is important, as it can enlarge “the shadow of the future” and urge leaders to exercise long-term thinking (Axelrod 1984: 126).

Some might say that states would never choose to purchase disarmament bonds, and they are not incorrect. Few states would likely pursue this individually, and states whose values are modeled by the Prisoner’s Dilemma or Deadlock will see little incentive to purchase disarmament bonds. But states with the appropriate values, if given the proper encouragement, could enter into a multilateral agreement to purchase these bonds. If a state is already able to recognize the value of disarmament, disarmament bonds could be able to decrease the risk enough to catalyze an actionable agreement.

Furthermore, it is important to recognize that values are not static. As Mutschler explains:

Political decision-makers always base their decisions upon a body of knowledge that is the result of interpretation. This knowledge structures their perceptions of reality by creating linkages between causes and effects. Thus, we should not take actors’ interests as given but rather explore the processes of knowledge-building that produce those interests. (2013: 52)

Even though some states currently hold views that preclude them from disarming via disarmament bonds, epistemic communities can help change the perspectives of states and state leaders (Mutschler 2013: 44). Though Mutschler and other scholars have often focused on shifting Deadlock Games to Prisoner’s Dilemmas, there is nothing preventing epistemic communities from framing disarmament as a Stag Hunt if that model proves effective.

Conclusion

Disarmament and game theory have had an intertwined history, and it is time to re-evaluate the way we model disarmament using game theory. Old models of disarmament have not provided actionable guidance for disarmament in reality, and thus a new perspective is needed. We must look beyond game tables and equilibria and more toward the economics of risk and reward. The Stag Hunt is the game theoretical model that provides the most hope for cooperation in multilateral disarmament, and it is through the Stag Hunt that a scheme can be designed to incentivize disarmament. One such plan would involve “disarmament bonds,” a financial instrument by which states pay an initial sum, agree to disarm, and then receive interest plus the initial principal for disarming; failure to disarm triggers default on the bond. This is just one hypothetical application of the principles of game theory and experimental economics towards incentivizing disarmament, and game theory still holds much relevance in multilateral disarmament in the modern day.

Afterword

With game theory and disarmament having been explored, it is now imperative to remember why disarmament is so important, lest its exigent need be forgotten. Violence is abhorrent. War and conflict bring unimaginable terror and destruction. These alone are categorical impetus enough to work to disarm our world and eliminate the scourge of war from this planet. But aside from the death tolls, the casualties, and the trauma, violence can be measured in dollars—according to the Global Peace Index, “The global economic impact of violence was $14.76 trillion PPP in 2017, equivalent to 12.4 per cent of global GDP” (2018: 4). It might seem heartless to measure violence in dollars when dolors plague those closest to fighting. But as Cicero once explained, “Endless money forms the sinews of war” (Goodreads). Money and war are intricately linked, and if we can disarm and decrease the damage from and the instances of war, then we will have “endless money” to divert to humanity’s most pressing problems. As the Secretary General of the UN, António Guterres, points out, $1.7 trillion was spent on militaries around the world this year (UNODA 2018). In comparison, fulfilling the Sustainable Development Goals (SDGs) requires $1.4 trillion per year (Gillis 2018). Humanity’s most noble goals—ending poverty and hunger, establishing renewable energy, providing universal and equitable education—these do not have to be dreams. These are considered by many to be impossible, but they are not impossible by the laws of physics—they are impossible only by the self-imposed laws of humans. Armament is the linchpin keeping the world’s most challenging problems from being solved. Disarmament could be what we need to change the world.

Total disarmament is far from a reality at present, but this does not mean small changes should not be celebrated. It is well known that violence begets violence, but if we can invest the money saved by disarmament in positive peace, then perhaps peace will engender peace. Destroying the instruments of war will save us from violence; reinvesting in peace can bring us to prosperity. Even small levels of disarmament can free money for new investments and change values of current and future leaders. The importance of disarmament is enshrined in Article 26 of the Charter of the United Nations:

In order to promote the establishment and maintenance of international peace and security with the least diversion for armaments of the world’s human and economic resources, the Security Council shall be responsible for formulating, with the assistance of the Military Staff Committee referred to in Article 47, plans to be submitted to the Members of the United Nations for the establishment of a system for the regulation of armaments. (1945)

The Charter exemplifies just how profoundly important disarmament is for humanity, and the Secretary General has taken it upon himself and his good offices to progress the disarmament agenda (UNODA 2018). It is essential that we utilize the good offices of game theory and economics to work towards cooperation in disarmament for the good of mankind.

Bibliography

Axelrod, R., 1984. The evolution of cooperation, New York: BasicBooks.

Borrie, J. & Randin, V.M., 2006. Thinking outside the box in multilateral disarmament and arms control negotiations, Geneva, Switzerland: UNIDIR.

Cassidy, J., 2015. The triumph (and failure) of John Nash’s game theory. The New Yorker. Available at: https://www.newyorker.com/news/john-cassidy/the-triumph-and-failure-of-john-nashs-game-theory [Accessed June 14, 2018].

Dixit, A.K., Skeath, S. & Reiley, D.H., 2015. Games of strategy, New York.: W. W. Norton.

Dubois, D., Willinger, M. & Nguyen, P.V., 2011. Optimization incentive and relative riskiness in experimental stag-hunt games. International Journal of Game Theory, 41(2), pp.369–380.

Engelmann, W., 1994. Conditions for disarmament: a game theoretical model. Group decision and negotiation, 3(3), pp.321–332.

Anon, Game Theory. Investopedia. Available at: https://www.investopedia.com/terms/g/gametheory.asp [Accessed June 13, 2018].

Gillis, M., 2018. Disarmament: a basic guide 4th ed.,

Goodreads, A quote by Marcus Tullius Cicero. Goodreads. Available at: https://www.goodreads.com/quotes/74326-endless-money-forms-the-sinews-of-war [Accessed June 14, 2018].

Hansel, M., Mutschler, M. & Dickow, M., 2018. Taming cyber warfare: lessons from preventive arms control. Journal of Cyber Policy, 3(1).

Institute for Economics and Peace, 2018. Global peace index 2018, Available at: http://visionofhumanity.org/app/uploads/2018/06/Global-Peace-Index-2018-2.pdf [Accessed June 14, 2018].

Jervis, R., 1978. Cooperation under the security dilemma. World Politics, 30(02), pp.167–214.

Keser, C., Ehrhart, K.-M. & Berninghaus, S.K., 1998. Coordination and local interaction: experimental evidence. Economics Letters, 58(3), pp.269–275.

Kuhn, S., 1997. Prisoner’s dilemma. Stanford Encyclopedia of Philosophy. Available at: https://plato.stanford.edu/entries/prisoner-dilemma/#Sym2t2PDOrdPay.

Mutschler, M.M., 2013. Arms control in space: exploring conditions for preventive arms control, Houndmills, Basingstoke, Hampshire: Palgrave Macmillan.

Myerson, R.B., 1997. Game theory: analysis of conflict, Cambridge: Harvard University Press.

O’neill, B., 1990. A survey of game theory models of peace and war. Handbook of Game Theory with Economic Applications. Available at: https://yorkspace.library.yorku.ca/xmlui/bitstream/handle/10315/1425/YCI0083.pdf?sequence=1&isAllowed=y [Accessed June 13, 2018].

Picardo, E., 2018. Advanced game theory strategies for decision-making. Investopedia. Available at: https://www.investopedia.com/articles/investing/111113/advanced-game-theory-strategies-decisionmaking.asp [Accessed June 13, 2018].

Polena, M., 2014. Does payoff dominance matter? An experiment. thesis. Institute of Economic Studies. Available at: file:///Users/Max/Downloads/BPTX_2011_2_11230_0_322719_0_124721 (1).pdf [Accessed June 14, 2018].

Anon, Private Conversation. June 2018. Geneva, Switzerland.

Ross, D., 1997. Game theory. Stanford Encyclopedia of Philosophy. Available at: https://plato.stanford.edu/entries/game-theory/#Mot [Accessed June 13, 2018].

Siang, C.K., 2010. Risk aversion and coordination in a simple stag hunt game: agent based modelling. SSRN Electronic Journal.

Swissinfo, Swiss secure mini-breakthrough at disarmament conference … SWI. Available at: https://www.swissinfo.ch/eng/nuclear-talks_swiss-secure-mini-breakthrough-at-disarmament-conference/44006248 [Accessed June 13, 2018].

United Nations, 1945. Charter of the United Nations, San Francisco, CA: United Nations. Available at: https://treaties.un.org/doc/publication/ctc/uncharter.pdf [Accessed June 13, 2018].

UNODA, 2018. Securing our common future: an agenda for disarmament, New York: UNODA.

UNOG, Disarmament. Where global solutions are shaped for you. Available at: https://www.unog.ch/80256EE600585943/(httpHomepages)/$first?OpenDocument [Accessed June 13, 2018].

Written by: Max Willner-Giwerc
Written at: Northeastern University
Written for: Professor Denise Garcia
Date written: June 2018

Further Reading on E-International Relations

• The Battle of Austerlitz and the Utility of Game Theory for Operational Analysis
• Game Theory and Non-Alignment: India’s Position in the Russia-Ukraine War
• The Prisoner’s Dilemma in Environmental Politics: One Model to Rule Them All?
• Gendered Perspectives and Nuclear Disarmament
• Laboring for Nuclear Disarmament? The Diplomacy of the Hawke-Keating Governments
• The Dangerous Double Game: The Coexistence of Nuclear Weapons and Human Rights