Since the Cold War, game theory as an analytical tool in International Relations has found widespread application in the study of strategic-level decision-making: arm or disarm, nuke first or wait, contribute to an alliance or free-ride. While concerning war and conflict, these are ultimately political, not military decisions. Although the subfield of Strategic Studies offers a particularly pertinent field of application for game theory, as military decision-making has been described as an area of “logical action” (Pareto) and “instrumental rationality” (Weber),[1] the study of the operational level of war with game-theoretical tools still receives less attention by academics and practitioners. This paper argues that game theory offers a unique, valuable toolkit for the analysis of military operations, as the almost infinite possibilities for modelling even complex battlefield scenarios enable historical and future operations to be simulated so that alternative courses of action can be compared and evaluated. Thereby it enables analysts and commanders to identify past mistakes and prevent future errors. First, several characteristics of game theory that favour its application for operational analysis are mapped out. Then, its utility for complex military scenarios such as deceptive manoeuvres in battle is demonstrated by analysing the Battle of Austerlitz through a game-theoretical lens. Lastly, the findings are summarised and it is argued that game theory should be taught and applied more widely in degree programmes, military academies, and by analysts across the field.

Game Theory in Operational Analysis

While not as prevalent as its use for strategic-level interactions, game theory has been applied both retrospectively for analysis and future-oriented for planning of military operations.[2] Due to several characteristics, it can serve as a valuable tool for insights into decision-making in battle and interactions between warring parties. Following, the most relevant characteristics are briefly highlighted.

First, i) formal modelling and ii) quantification of payoffs in game theory allow one to systematically trace, evaluate, and compare courses of action in and outcomes of military operations.[3] Moreover, by considering battles as iii) dynamic sequences rather than as unitary events, game theory can account for different phases, repeated actions, learning, and adaptation during engagements.[4]  It can also capture the iv) strategic interdependence of parties, and analyse how choices of one influence and are influenced by others.[5] Game theory is also suitable for situations in which commanders make decisions based on v) imperfect, incomplete, or asymmetric information—what Clausewitz called a “fog of greater or lesser uncertainty.”[6] By their very design, game-theoretical models are also well-suited to include vi) counterfactuals as battle scenarios that deviate from actual events.[7] For cases involving alliances, game theory further helps to understand vii) coordination and cooperation in war by assessing how allies coordinate or make joint decisions to pursue common objectives.

Notwithstanding its various advantageous characteristics, the use of game-theoretical models for the analysis of military operations is subject to criticism. Some authors, like Berkovitz and Dresher, argue that game theory is “not a helpful device”[8] for operational analysis because its imperfect, oversimplified models would distort the findings too much. Others, like Elster, reject the underlying concept of rational choice theory and idealised assumptions about actor’s behaviour altogether, believing their empirical shortcomings would disqualify them from the proper analysis of historical events.[9] Similarly, Caballero et al. criticise the disregard of overconfidence, emotional factors, and uncertainty in the concept of perfect rationality as detrimental to its applicability to military operations, proposing behavioural game theory as an alternative.[10]

This brief overview has shown that, by its very nature, game theory can be a valuable tool for the structured, formalised analysis of the inherently chaotic endeavour of war. Nonetheless, it is not without shortcomings. Following, the utility of game-theoretical models for the analysis of military operations shall be further illuminated.

The Battle of Austerlitz from a Game-Theoretical Perspective

The Battle of Austerlitz took place on 2nd December 1805 between Napoleon’s Grande Armée and Austrian and Russian forces of the Third Coalition, led by Francis II and Alexander I. Outnumbered and on lower terrain, Napoleon deceived the Allies into believing his right flank was numerically weak, vulnerable, and about to retreat.[11] Through this deceptive manoeuvre, Napoleon lured his opponents into advancing on their left flank, thus weakening their centre and giving up the high ground, which he exploited through a thrust in the resulting gap, followed by an encirclement of the Allied forward left flank.[12] Ultimately, the French decisively defeated the Coalition armies, marking the end of the War of the Third Coalition.

Because of its distinct phases and deception causing information discrepancies between the parties, the Battle of Austerlitz is ideal for demonstrating the utility of game theory for insights into decision-making processes and strategic interactions in military operations.

Modelling Austerlitz: A Deception Game

While many game-theoretical models assume that players are aware of all possible strategies and payoffs, parties in real-world conflicts seldom possess perfect information about their opponent’s strategies and, especially, their payoffs. In the Battle of Austerlitz, due to Napoleon’s deception, the Allies had imperfect (unaware of actions taken by Napoleon), incomplete (unaware of real strategies and payoffs), and asymmetric information (Napoleon knew more than them).

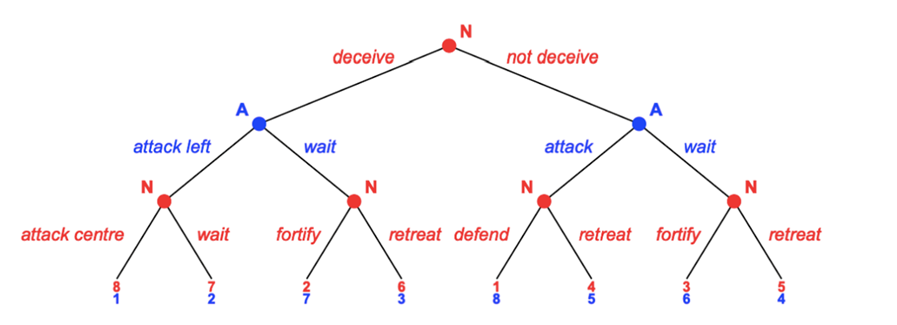
Various games allow to depict the particularities of such real-world scenarios more clearly, of which the deception game is most suitable for this case.[13] Following, the deception game by Baston and Bostock is adapted to the Battle of Austerlitz.[14] In a deception game, one player, the deceiver, has perfect information on the real game (X), distorts information, and presents a modified game (Y) to the other player.[15] For the Battle of Austerlitz, two two-player, zero-sum games in extensive form are modelled between Napoleon (N) on one side (the deceiver) and the Allies (A) on the other (the deceived).

The Real Game

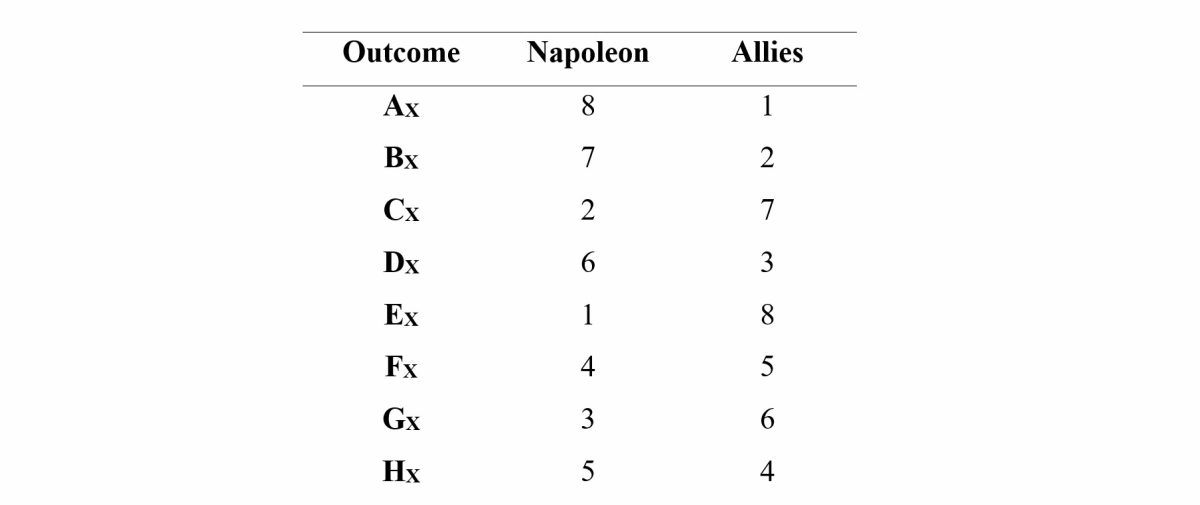
In the real game X (see Fig. 1),[16] Napoleon has eight and the Allies have four pure strategies:

S_NX: {(deceive, attack centre, fortify), (deceive, attack centre, retreat), (deceive, wait, fortify), (deceive, wait, retreat), (not deceive, defend, fortify), (not deceive, defend, retreat), (not deceive, retreat, fortify), (not deceive, retreat, retreat)}

S_AX: {(attack left, attack), (attack left, wait), (wait, attack), (wait, wait)}

The game has eight outcomes, designated with capital letters from left to right: A_X, B_X, C_X, D_X, E_X, F_X, G_X, and H_X. Following, the outcomes are ranked according to the player’s preference order and then translated into payoffs. Because it is a zero-sum game, every gain of Napoleon is a loss to the Allies. Thus, payoffs for the Allies are reversed.

Napoleon’s deception plan is represented by A_X, from which he receives the most utility because his deception draws the Allies into the trap on his right flank, which in turn enables his push into the exposed Allied centre. This approach was arguably the only way to counter his numerical and terrain disadvantage, and ultimately led to his victory.

B_X is the next preferable outcome for Napoleon because his deception is successful and the Allies attack his right flank as intended. By waiting instead of immediately exploiting the centre gap, he retains all options, including drawing the Allied centre into close range, encircling and cutting off the advanced Allied left, or flanking the Allies to their right.

Then, D_X is the next preferable outcome for Napoleon, because while the Allies do not fall for his deception, they wait and provide him with the time for an orderly retreat to fight another day in full strength. He retains control over his troops, does not suffer any losses, and can mass forces at another place and time, where he is not as vulnerable in manpower and position. H_X, the next preferable outcome for Napoleon, is the same scenario only that Napoleon does not attempt to deceive the Allies, thus has no prospect of winning in the first place—it’s better to try and fail than not to try at all.

F_X is the next preferable outcome for Napoleon. He does not deceive, the Allies attack him with full force from high ground, and he retreats. While he is not decisively defeated in battle and does not suffer considerable losses, it represents a humiliation and loss of prestige. Still, he will be able to fight another day and retain future options.

In G_X, the next preferable outcome for Napoleon, he does not deceive, the Allies wait and leave him time to fortify his positions. By creating obstacles and strengthening his position, he can compensate a little for the Allies’ advantages but still must fight a larger enemy from an unfavourable position. In this scenario, Napoleon would have probably lost the battle. C_X represents the same scenario, only that Napoleon attempts to deceive, the Allies do not fall for it, and he uses the time to strengthen his position. Through the failed deceptive manoeuvre, Napoleon exposes his right flank and, to regroup his troops, close his ranks, and then consolidate his position, must put in considerably more effort than in G_X, which makes him vulnerable to attack and contributes to confusion and fatigue among the soldiers.

E_X represents the least preferable outcome to Napoleon because he does not deceive, the Allies attack with full force, and he must defend with fewer men from a detrimental position. Most likely, the French would have decisively lost the battle and thus the war.

This assessment yields the following preference order for Napoleon and the Allies, translated into payoffs in Table 1:

U_NX = A_X ≻ B_X ≻ D_X ⪰ H_X ≻ F_X ≻ G_X ⪰ C_X ≻ E_X

U_AX = E_X ≻ C_X ⪰ G_X ≻ F_X ≻ H_X ⪰ D_X ≻ B_X ≻ A_X

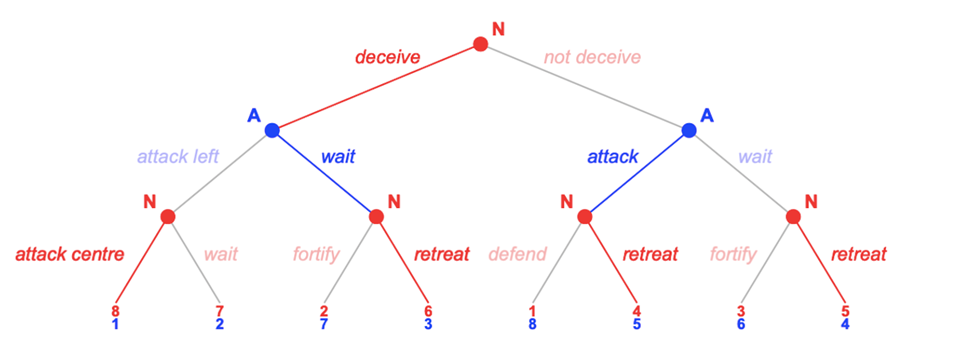
If game X is played with perfect information, both players behave optimally, and all threats are credible, backward induction yields the subgame perfect equilibrium D_X {deceive, wait, retreat} with a payoff of (6, 3) (see Fig. 2). This means that in the hypothetical case that the Allies would have anticipated Napoleon’s deception or would have been informed about it by a spy, they would have waited in their advantageous position, and Napoleon would have been forced to retreat without a battle.

The Deception

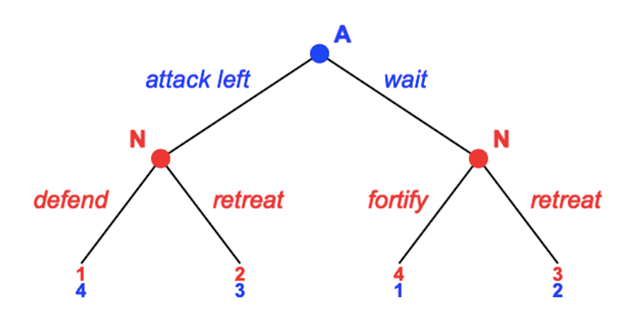
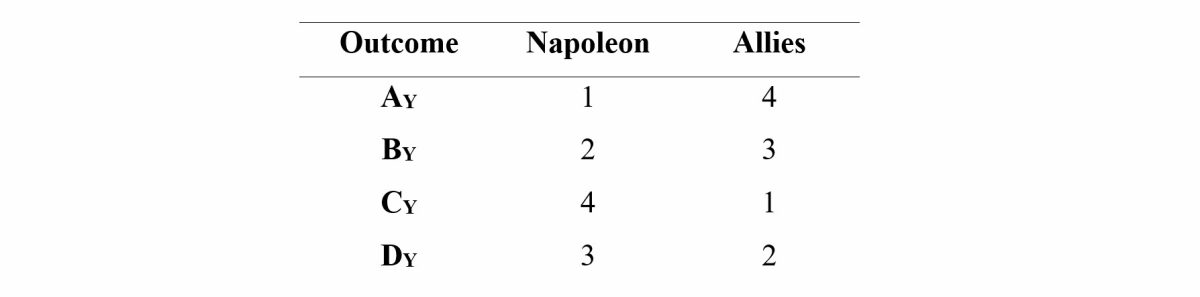
Through his deceptive manoeuvre, Napoleon presents the distorted game Y to the Allies, in which strategies and payoffs are different than in X (see Fig. 3). In Y, Napoleon has four and the Allies have two pure strategies:

S_NY: {(defend, fortify), (defend, retreat), (retreat, fortify), (retreat, retreat)}

S_AY: {attack left, wait}

Through deception, Napoleon presents four supposed outcomes to the Allies: A_Y, B_Y, C_Y, and D_Y. Following, payoffs are assigned to the outcomes. Again, because it is a zero-sum game, Allied gains are losses for Napoleon.

In outcome A_Y, the most preferable for the Allies, they attack Napoleon’s supposedly weak right flank with their left and, because they have the higher ground and more soldiers, break the lines, and cause a rout of the French. This allows the Allies to encircle Napoleon from the left and thrust into his centre with their centre and right troops. This would have resulted in a decisive victory for the Allies and a devastating French defeat, which probably would have ended the war in favour of the Allies.

The difference between B_Y, the next preferable outcome for the Allies, and A_Y is that Napoleon retreats, making the Allies victorious but enabling the French to regroup, replenish units that have suffered casualties in their retreat, and fight another day. While it would have been a tactical victory, it would not have ended the war. The same goes for D_Y, where the Allies are not exploiting Napoleon’s supposed vulnerability but wait instead, which leaves Napoleon free to withdraw in full strength without any casualties, delaying a decision to the future.

Lastly, in C_Y, the Allies do not exploit Napoleon’s supposed vulnerability but wait instead, thereby allowing him to compensate for his disadvantages. While the Allies could have still won the battle, they would have lost the opportunity to exploit their opponent’s weakness and would have suffered significant casualties. Letting the Grande Armée retreat and instead seize future advantages would have been preferable to a high-risk/high-casualty endeavour.

This assessment yields the following preference order for Napoleon and the Allies, translated into payoffs in Table 2:

U_NY = C_Y ≻ D_Y ≻ B_Y ≻ A_Y

U_AY = A_Y > B_Y > D_Y > C_Y

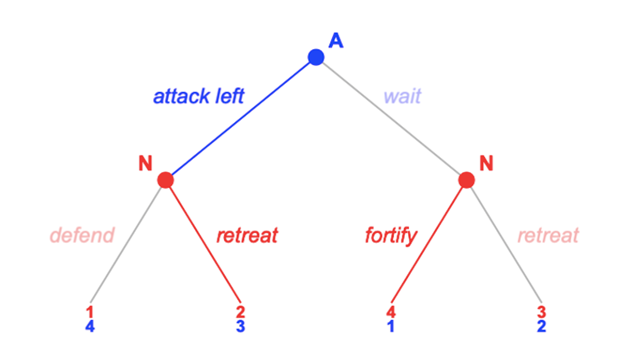
If Y had been the actual scenario and not a deception, it would have yielded the subgame perfect equilibrium B_Y {attack left, retreat} with a payoff of (3, 2) (see Fig. 4). Therefore, if the Allied assumption about Napoleon’s vulnerability would have been correct, an attack on his weak right flank would have forced the French to retreat, making the Allied decision perfectly rational given their (flawed) assumptions.

Assessment

The game-theoretical analysis of the Battle of Austerlitz has aptly demonstrated how deception in battle works. The Allied advance against Napoleon’s right flank was not an ill-considered blunder, but the best strategy under false assumptions. For Napoleon, on the other hand, deception was the only way to induce the Allies to push forward with their left and give up their numerical and terrain advantages—without deception or with perfect information, Napoleon would have had to retreat, and the war would have continued.

Through the transfer of the battle into a formal model and by quantifying payoffs, it was possible to trace, compare, and evaluate potential courses of action throughout the dynamic sequences of the operation. Moreover, the strategic interdependence of both actors has been demonstrated by showing how Napoleon’s deception influenced the thought process of the Allies under imperfect, incomplete, and asymmetric information, which in turn influenced Napoleon’s decisive encirclement. Moreover, it was possible to incorporate the counterfactual scenarios of what would have happened if Napoleon had not deceived the Allies, if the Allies would not have fallen for the deception, or if the Allies would have attacked in full force.

Conclusion

In conclusion, it can be reiterated that game theory provides a very valuable toolkit for academics and practitioners committed to the rigorous analysis of one of the most complex human endeavours—war. Therefore, graduate programmes, military academies, and analysts in the field of strategic studies should adopt game theory even more as a standard tool, if only to improve a common understanding of why and how commanders make decisions in battle and prevent past mistakes from being repeated.

Every model or theory we use to explain human interaction simplifies, thus we should treat all findings with caution. Nonetheless, the characteristics of game theory and its versatility make it an instrument that can be carefully adapted and refined to the needs and demands of military operations—this is as good as it gets.

---

Figures and Tables

Notes

[1] Both cited in Mongin (2017, pp. 3f.).

[2] See Haywood (1954), Berkovitz and Dresher (1959); Mongin (2017); Caballero et al. (2020).

[3] Haywood (1954, p. 383).

[4] Lunde (2020, p. 29).

[5] Caballero et al. (2020, pp. 9, 18); Lunde (2020, pp. 7-10).

[6] von Clausewitz [1832] (1976, p. 101).

[7] Lunde (2020, p. 29).

[8] Berkovitz and Dresher (1959, p. 612); also Martin (1978, p. 95).

[9] Elster (2000).

[10] Caballero et al. (2020, pp. 5, 20).

[11] Mettra and Jacquemin (2016, p. 29f.).

[12] See von Stutterheim (1807).

[13] Others include, for example, hypergame theory or Bayesian signalling games.

[14] See Baston and Bostock (1988); also Fristedt (1997).

[15] Baston and Bostock (1988); Spencer (1973).

[16] Game Theory Explorer v2.2.6 is used for all game trees, see Savani and von Stengel (2015).

Bibliography

Baston, V. J., and Bostock, F. A. (1988). Deception games. International Journal of Game Theory, 17(2), pp. 129-134.

Berkovitz, L. D., and Dresher, M. (1959). A Game-Theory Analysis of Tactical Air War. Operations Research, 7(5), pp. 599-620.

Caballero, W. N., Lunday, B. J., Deckro, R. F. (2020). Leveraging Behavioral Game Theory to Inform Military Operations Planning. Military Operations Research, 25(1), pp. 5-22.

Dixit, A. K., and Nalebuff, B. J. (2008). The Art of Strategy. W. W. Norton.

Elster, J. (2000). Rational Choice History: A Case of Excessive Ambition, American Political Science Review, 94(3), pp. 685-695.

Fristedt, B. (1997). The deceptive number changing game, in the absence of symmetry. International Journal of Game Theory, 26(2), pp. 183-191.

Haywood, O. G. (1954). Military Decision and Game Theory. Journal of the Operations Research Society of America, 2(4), pp. 365-385.

Lunde, N. A. (2020). The Use of Game Theory at the Operational Level. US Army Command and General Staff College.

Martin, B. (1978). The Selective Usefulness of Game Theory. Social Studies of Science, 8(1), pp. 85-110.

Mettra, M., and Jacquemin, T. (2016) The Battle of Austerlitz: The Battle That Changed the Map of Europe. 50 Minutes.

Mongin, P. (2017). A Game-Theoretic Analysis of the Waterloo Campaign and Some Comments on the Analytic Narrative Project. MPRA Paper, No. 78029.

Rubinstein, A. (1989). The Electronic Mail Game: Strategic Behavior Under ‘Almost Common Knowledge’. The American Economic Review, 79(3), pp. 385-391.

Savani, R., and von Stengel, B. (2015). Game Theory Explorer—Software for the Applied Game Theorist. Computational Management Science, 12, pp. 5-33.

Spencer, J. (1973). A deception game. American Mathematical Monthly, 80, pp. 416-417.

von Clausewitz, C. [1832] (1976). On War. M. Howard and P. Paret (transl. and ed). Princeton University Press.

von Stutterheim, K. (1807). A Detailed Account of the Battle of Austerlitz. Project Gutenberg.

Further Reading on E-International Relations

• Game Theory and Disarmament: Thinking Beyond the Table
• Risk Theory vs. Securitisation: An Analysis of the Global Surveillance Program
• Globalisation, Agency, Theory: A Critical Analysis of Marxism in Light of Brexit
• Old Wine, New Bottles: A Theoretical Analysis of Hybrid Warfare
• The Dangerous Double Game: The Coexistence of Nuclear Weapons and Human Rights
• “In sight of surrender”: Critical Analysis of the 2022 Sanction Regime on Russia